|
[?]Subscribe To This Site
|
Steel Beam Sizing FormulaThe formula for steel beam sizing or steel beam design is section modulus (S) = moment (M)/allowable yield stress (Fy) or in short S=M/Fy. The tables for structural steel sizes such as steel i beam sizes show the steel beam dimension for a steel i beam where S can be selected to satisfy the design. The moment is calculated using the formula M=wL^2/8 for uniformly loaded beam, where L is the unsupported length of the beam and w is the load applied. As this beam moment formula suggests, the longer the span and heavier the load, the more the moment becomes.If you want to minimize the depth of a beam, two of the possible solutions are reducing the unsupported length L or reduce the weight applied to the beam. For a beam loaded with a point load for instance if you need a steel beam to support an air condition unit that weighs 2,000 pounds. The moment formula will be M = PL/4.
To illustrate this process, let’s verify the beam used for the framing plan above. Please refer to concrete footing design for detail information on how the load was calculated. The load used to design the footing is the same load used for the beam design. The total load is 48.2 psf with tributary width 12'-7". Multiplying the two yields 606.5 plf. The clear span is 19 ft. Substituting these to the moment formula: M=wL^2/8 = 606.5*19^2/8 = 27,369 lb-ft x 12/1000 (multiply by 12 to convert to inches / divide by 1000 to convert to kips) = 328.43. The allowable stress is .66*50 = 33 ksi.The section modulus required is S = 328.43/33 = 9.95 in^3 (cubic inches). S for W12x26 is 33.4 which is much bigger than 9.95, therefore the selected beam is ok. A W12x14 with S = 14.9 would be ok too but was not available at the time of construction. W12x26 was selected because it was the smallest beam available at the time of construction. Back to steel beam sizing |
|
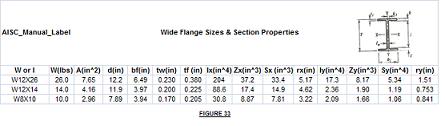The allowable yield stress per code is 66 percent of yield stress which is .66x50 for 50 ksi steel for wide flange sections. If you are estimating the capacity of older steel or steel where yield stress is not known, use Fy = 36 ksi.
